How to use moment of inertia calculator for any structure

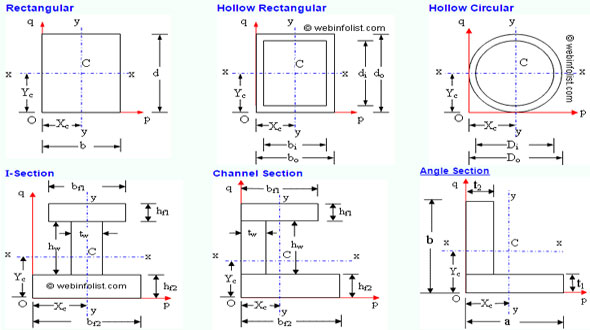
Moment of inertia alias second moment of area plays a significant role in ascertaining the stability of beams and columns concerning a structural system. Moment of inertia provides good resistance against bending and torsion of a structure. It is also necessary to detect slope and deflection of beams.

Moment of inertia calculator specifically designed to facilitate assessing moment of inertia and other geometrical properties regarding plane sections of beam and column. It is possible to copy and paste the results from these calculators in the document file. The users can choose from the list of plane sections provided underneath or visit.

This moment of inertia can be used to make calculation of area, centroid, moment of inertia, section modulus and radius of gyration for Rectangular, Circular, Angle, T , Channel and I sections of structural members.

(i) This calculator selects the origin "O" of reference axes at the intersection of the horizontal axis (o-p) overlapping with the lower-most edge of the section and vertical axis (o-q) overlapping with the utmost left edge of the section. All the distances have to be put in "cm" and the calculated values are obtained in terms of equivalent units of "cm". If the distances are provided in "inch" the values should have been in the equivalent units in "inch".
(ii) The position of centroid 'C" is estimated in terms of its coordinates with regard to origin of axes "O".
(iii) The moment of inertia is computed about the x-x axis and y-y axis passing by the centroid of the section.
(iv) For the hollow rectangular or hollow circular sections, the section should be uniform about both x-x and y-y axes i.e. with constant thickness.
(v) In case of I section and T section, the section should be equal about y-y axis.

Click on the following link to get the brief guidelines for using Instructions for Moment of Inertia Calculator