How to Calculate the Volume of a Frustum

A frustum can be created from a right circular cone by cutting off the tip of the cone using a cut perpendicular to the height, developing a lower base and an upper base which are circular and parallel.

Suppose,
h is taken as height

R is taken as the radius of the lower base

r is taken as the radius of the upper base.

The Formula:

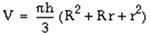
Determine the volume of a frustum of a cone whose ends contain radii of 12 cm and 8 cm and the height is 5 cm.

Assume there is a cone having the base of 12 cm radius and a height of 15 cm. The volume of this cone is calculated as (1/3)(22/7)*12^2*15 = 2262.857143 cu cm.

Next from the cone, take out a smaller cone of radius 8 cm. From the same triangles (generated by creating a section through the apex of the cone and right through the diameter of the base):

8/12 =h/15, or h = 8*15/12 = 10 cm.

The smaller cone that is taken out with a radius 8 cm and height 10 cm, and its volume is calculated as follow:
(1/3)(22/7)*8^2*10 = 670.4761905 cu cm.

The height of the frustum is calculated as 15–10 = 5 cm

Therefore, the volume of the frustum of the cone is 2262.857143 - 670.4761905 = 1592.380953 cu cm.

Also Read: How To Do A Concrete Slump Test

The formula of a frustum is V = (pi)h[R^2 +Rr + r^2]/3, where

R denotes bigger radius

r denotes smaller radius

h denotes height of the frustum.

Applying the formula, V = (22/7)*5[12^2+12*8+8^2]/3 = 1592.380953 cu cm.

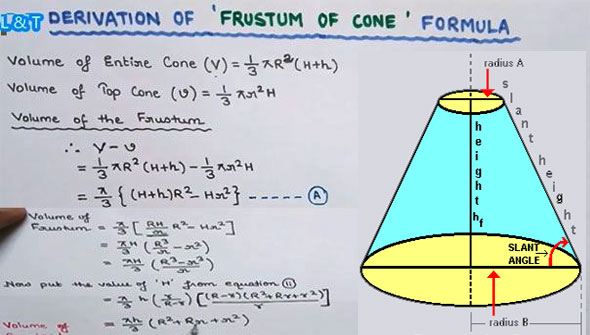
To get more clear idea, go through the following exclusive video tutorial presented by the renowned civil engineer Mr. Mukesh Sah.

Video Source: L & T - Learning Technology