Details of shear stresses in beam

Shear force means any force that attempts to shear-off the member.

Shear force belongs to an unbalanced force parallel to the cross-section, primarily vertical and remains either right or left of the section.

To combat the shear force, the component will produce the defiant stresses, which are called as shear stresses (τ)

τ = shear force/cross sectional area = S/A

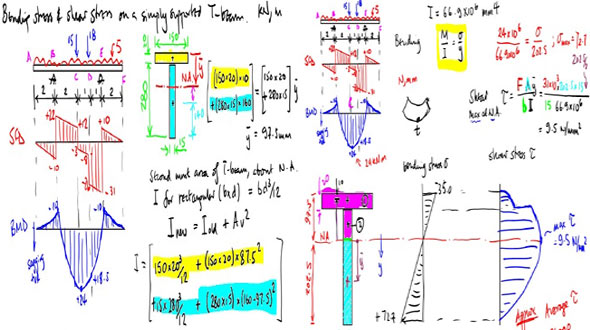
Shear stresses in beams

Shear stresses are generally highest at the neutral axis of a beam (always when the depth is constant or when the depth at neutral axis is least for the cross section, like for I-beam or T-beam), but zero at the top and bottom of the cross section since the normal stresses are maximum/minimum.

When a beam is dependent on loading, both bending moments (M) and shear forces (V) function on the cross section.

Suppose, there is a beam with rectangular cross section. It is presumed that the shear stresses (τ) function parallel to the shear force (V).

Shear stresses on one side of a component are followed by shear stresses of identical magnitude that functions on perpendicular faces of a component. So, the horizontal stresses are produced among the horizontal layers of the beam together with the vertical shear stresses on the vertical cross section.

Horizontal shear stress happens because of the differentiation in bending moment along the length of beam.

Suppose, there are two sections as PP’ and QQ’, the distance among them is presented as ‘dx’, the sections bear bending moment (M) and shear forces (S) and ‘M + ∆M and S + ∆S’ correspondingly.

Suppose, there is an elemental cylinder P”Q” with area ‘dA’ among section PP’ and QQ’. The distance for the cylinder from neutral axis is ‘y’.

So, bending stress at P’’ will be as follow :-

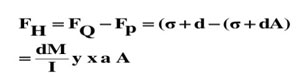
This unbalance horizontal force is countered by the cylinder along its length as shear force. This shear force functioning along the surface of cylinder is parallel to the primary axis of beam that produces horizontal shear stresses in beam.